Wstęp
Ada Lovelace, znana córka pisarza lorda Byrona i uważana jako pierwsza programistka na świecie. W swoim okresie miała pieniądze i wykształcenie dzięki któremu mogła realizować swoje marzenia. Mało jednak kto wie jak skończyła. W wieku 36 lat zmarła na raka, i mimo bogactwa z olbrzymimi długami spowodowanych hazardem.
Ada wierzyła że w jakiś sposób dzięki matematyce będzie w stanie wygrywać na wyścigach konnych co niestety dla niej nie skończyło się dobrze. Hazard do dziś istnieje i aktualnie jest jeszcze łatwiej dostępny niż kilkadziesiąt lat temu. Teraz nie musimy wybierać się do Las Vegas by móc grać w kości czy ruletkę. Wystarczy tylko odwiedzenie odpowiedniej strony.
Aktualnie większość (jak nie każdy) który w pewnym stopniu interesuje się matematyką może pomyśleć czy nie dałoby się wykorzystać swojej wiedzy i stworzyć system który zapewniłby nam stały dopływ gotówki 😃 Może istnieje jakiś algorytm dzięki któremu możemy zapewnić sobie wygraną. W dodatku mamy przecież komputery i języki programowania typu Python. Czy nie lepiej najpierw zrobić sobie obliczenia na sucho i przeprowadzić testy na tysiącach symulacji zanim weżmiemy swoje oszczędności i pomnożymy je dzięki Matematyce.
W artykule będe opisywał tylko losowe gry hazardowe. Nie ma tu takich gier jak Poker ponieważ on mimo elementu losowości zależy także od umiejętności i nawet w przypadku słabych rozdań pozwala zdolnym graczom wygrywać.
Przykładem niech będzie gra w stylu rzutu monetą (kostką). Komputer losuje wartość od 0 do 100 i jeśli wytypowaliśmy że będzie np: większa niż 50 i tak jest to wygrywamy, jeśli nie to przegrywamy. Oczywiście przy typowaniu mniejszych zakresów stawka jest odpowiednio niższa. I analizując tak przedstawiają się niektóre stawki:
| Zakładamy że wynik jest mniejszy od | Szansa wygranej | Wygrana od zakładu (bet) |
|---|---|---|
| 24.75 | 24.75% | 4.00x |
| 33.00 | 33.00% | 3.00x |
| 49.50 | 49.50% | 2.00x |
| 50.00 | 50.00% | 1.98x |
| 33.00 | 33.00% | 3.00x |
| 24.75 | 24.75% | 4.00x |
| 66.00 | 66.00% | 1.50x |
| 75.00 | 75.00% | 1.32x |
| 90.00 | 90.00% | 1.10x |
Warto zauważyć że przy stawce 50% jest to tak naprawdę gra w rzut monetą. Powiedzmy że gramy z kolegą, stawiam 1 złotówkę i typuje reszkę. Jeśli wypadnie reszką kolega oddaje mi 0.98zł czyli razem mam 1.98zł. Natomiast jeśli on wygra zabiera moją złotówkę czyli dostaje łącznie 2 złote. Od razu widać że gra nie jest do końca uczciwa, w przypadku przegranej oddajemy więcej niż kasyno. Te zależności widać także przy innych zakładach i jest to tzw. marża kasyna. Jeśli zagramy wiele razy możemy przypuszczać że udział orłów i reszek będzie dążył do 50% (jeśli jest to idealnie symetrycznie moneta). Tak więc grając cały czas w przypadku równego podziału dostałbym za reszkę 50% wszystkich wpłaconych pieniędzy. Czyli tyle samo co wpłaciłem. Na końcu obaj wyszlibyśmy na 0. Natomiast w przypadku gdy dostajemy mniej co wyniknie z naszych symulacji w przypadku tak prostego algorytmu nasza kwota będzie się systematycznie pomniejszać.
Poniżej przedstawiam dwie części. Pierwszy z nich to Gra. Jest to napisana przeze mnie kopia systemu ze strony darmowego kasyna do testów w której możemy symulować nasze zachowania na podstawie 3 algorytmów.
- Pierwszy to automat który jest kopią automatu ze stron z zakładmi
- Drugi jest moim własnym systemem tablicowych gdzie możesz samemu ustalić co robić po każdej wygranej/przegranej, o ile podnieść stawkę i z jakim prawdopodobieństwem zagrać.
- Trzeci jest systemem Labouchere który jest popularnym systemem w grach hazardowych takich jak ruletka.
Druga część pokazuje jak można takie algorytmy sobie zasymulować w Pythonie i może przed zobaczyć czy nasze cudowny algorytm rzeczywiście działa 😃
Na koniec wstępu mała dygresja:
Polskie Prawo
Według polskiej ustawy wszelkie gry hazardowe online które nie pochodzą od podmiotu wyznaczonego przez państwo (Totalizator Sportowy) są zabronione. W artykule wykorzystałem darmowe strony do grania które służą tylko do grania i nie wymagają wkładu pieniężnego.
Gra
Automated betting
Polega on na automatycznym zwiększaniu wartości zakładu po przegranej albo wygranej.
Wejścia:
- START CASH: kwota początkowa
- START BET AMOUNT: początkowa stawka
- NUMBER OF RUNS: liczba uruchomień
- GAME: Rodzaj gry i prawdopodobieństwo wygranej
- NUMBER OF ROLLS: liczba rzutów
- ON LOSS: co się dzieje po przegranej
- Reset to base: powrót to początkowej wartości
- Increasy by %: Zwiększenie wartości o podany %
- ON WIN: co się dzieje po wygranej
- Reset to base: powrót to początkowej wartości
- Increasy by %: Zwiększenie wartości o podany %
Table System
W odróżnieniu od Automated Betting można także ustawić co robimy po przegranej pierwszej, drugiej, itp…
Wejścia:
- START CASH: kwota początkowa
- START BET AMOUNT: początkowa stawka
- NUMBER OF RUNS: liczba uruchomień
- GAME: Rodzaj gry i prawdopodobieństwo wygranej
- NUMBER OF ROLLS: liczba rzutów
- ON LOSS: co się dzieje po przegranej
- 1 |: Numer przegranej
- LOSS: Ile przegraliśmy
- Reset to base: powrót to początkowej wartości
- Increasy by %: Zwiększenie wartości o podany %
- GAME: Jaką gre ustawić po przegranej
- BET: Ile wynosi stawka
- TO WIN: IIle można wygrać i jaki jest całkowity zysk po wygraniu
- ON WIN: co się dzieje po wygranej
- 1 |: Numer wygranej
- WIN: Ile wygraliśmy
- Reset to base: powrót to początkowej wartości
- Increasy by %: Zwiększenie wartości o podany %
- GAME: Jaką gre ustawić po przegranej
- BET: Ile wynosi stawka
- TO WIN: IIle można wygrać
Wyjście:
- Run: Który to rzut
- Avg Cash: Średnia ilość gotówki w danym rzucie
- Avg Profit from start:: Średni zysk od początku
- Avg win: Średnia wygrana i procent wygranych
- Avg loss: Średnia przegrana i procent przegranych
- Avg Single profit: Średni zysk w aktualnym rzucie
- Highest Bet: Najwyższa postawiona stawka i procent ile razy się trafiła
- Highest Losses Cnt: Najwyższa ilość, ile razy przegraliśmy pod rząd
- Bancrupt: % udziału uruchomień które mają mniej pieniędzy niż wymagany zakład
Labouchere
Wejścia:
- START CASH: kwota początkowa
- NUMBER OF RUNS: liczba uruchomień
- SYSTEM NUMBERS: Liczby do systemu Labouchere
Wyjście:
- Win rolls:: Ilość wygranych i udział w procentach
- Loss rolls:: Ilość przegranych i udział w procentach
- Avg profit:: Średni zysk
- Rolls: Liczba rzutów po której została zakończona gra
- %: Procent i ilość udziału danej ilości rzutów
- Avg Profit: Średni zysk
- Avg Profit * % : Średni zysk pomnożony przez udział
- Highest Bet: Najwyższy zakład
- Highest list: Lista w przypadku przegranej dla najwyższego zakładu
Gra
Artykuł
Definicja
Zacznijmy od definicji Gry. Najpierw należy stworzyć funkcję która nam zwróci kwotą którą wygraliśmy na plus (jeśli wygramy) lub na minus jeśli przegramy.
import random as r
games = {
"1.10": { 'count': 1.10, 'chance': 0.90 },
"1.32": { 'count': 1.32, 'chance': 0.75 },
"1.50": { 'count': 1.50, 'chance': 0.66 },
"1.98": { 'count': 1.98, 'chance': 0.50 },
"2.00": { 'count': 2.00, 'chance': 0.495 },
"3.00": { 'count': 3.00, 'chance': 0.33 },
"4.00": { 'count': 4.00, 'chance': 0.2475 },
}
def play(bet,game_count):
result = r.random()
game = games[game_count]
if(result <= game['chance']):
return bet * game['count'] - bet
return -bet
I dla przykładu:
play(1,"1.50")
play(1,"1.50")
play(1,"1.50")
-1
0.5
-1
[play(1,"1.50") for i in range(5)]
[-1, -1, 0.5, 0.5, 0.5]
Problemem z takimi funkcjami jest to że nie są deterministyczne 😦 To znaczy nie możemy ich testować tak jak są ponieważ za każdym razem mogą zwrócić inny wynik. Więc w przypadku testów dla takiej funkcji warto przed każdym uruchomieniem ustawić ziarno dla funkcji random.
print(play(1,"1.10")) # -1 or 0.1 random
print(play(1,"4.00")) # 3.0 or -1 random
r.seed(123)
print(play(1,"1.10")) #always 0.1000
print(play(1,"4.00")) #always 3.0
r.seed(123)
print(play(1,"1.10")) #always 0.1000
print(play(1,"4.00")) #always 3.0
Na początek zaaplikujemy algorytm automatyczny znany z wielu gier kasowych. Polega on na zwiększeniu bądż zmniejszeniu zakładu gdy przegramy albo wygramy. Wartość -1 oznacza że wracamy do puli początkowej.
- start_bet - początkwy zakład
- bet - aktualny zakład
- result - ile wygraliśmy, wartość na minusie oznacza że przegraliśmy
- on_loss - O ile podnieść wartość po przegranej . Wartość -1 oznacza powrót do wartości początkowy
- on_win - O ile podnieść wartość po wygranej. Wartość -1 oznacza powrót do wartości początkowy
Cały algorytm wygląda następująco
# on_loss/on_win = -1 return to base
def auto_method(start_bet, bet, result, on_loss, on_win):
if(result > 0):
return start_bet if on_win < 0 else bet+bet*on_win
else:
return start_bet if on_loss < 0 else bet+bet*on_loss
print(auto_method(1, 10,-0.5, -1, -1)) # 1
print(auto_method(1, 10,-0.5, 1, -1)) # 20
print(auto_method(2, 10,0.5, -1, -1)) # 2
print(auto_method(2, 10,0.5, 1, 2)) # 30
Warto teraz zrobić sobie automat który zasymuluje grę za każdym razem grając i wyrzucając wynik tak żeby póżniej można było sporządzić wyniki.
import pandas as pd
import numpy as np
# on_loss/on_win = -1 return to base
def auto_run(start_bet = 1, cash = 100, game_count = "2.00", rolls = 50,
on_loss = -1, on_win = -1, simulation = 0):
#results = pd.DataFrame(columns=['roll','cash_before','bet','bancrupt', 'result','cash'],dtype=float)
bet = start_bet
result_list = []
for i in range(rolls):
cash_before = cash
if(cash_before < bet):
result_list.extend([[i+ii, cash, 0, 1.0, 0, cash, simulation] for ii in range (rolls-i) ])
break
result = play(bet, game_count)
cash += result
result_list.append([ i,cash_before, bet, 0, result, cash, simulation ])
bet = auto_method(start_bet,bet,result,on_loss,on_win)
return pd.DataFrame(result_list, columns=['roll','cash_before','bet','bancrupt', 'result','cash', 'simulation' ],dtype=float)
Pojedyńcze uruchomienie zwraca pojedyńcze wydarzenie, i jak można się domyśleć czasami wygrywamy i czasami przegrywamy. Popatrzmy na przykład na zwykłe podwajanie stawki on_loss = 1 przy graniu na typowym zakładzie game_count = "2.0", czyli zwraca nam dwukrotność, ale szansa wygrania wynosi 0.495.
auto_run(game_count = "2.00",cash = 100, start_bet = 1, on_loss = 1, rolls = 10)
roll cash_before bet bancrupt result cash simulation
0 0.0 100.0 1.0 0.0 1.0 101.0 0.0
1 1.0 101.0 1.0 0.0 -1.0 100.0 0.0
2 2.0 100.0 2.0 0.0 -2.0 98.0 0.0
3 3.0 98.0 4.0 0.0 4.0 102.0 0.0
4 4.0 102.0 1.0 0.0 -1.0 101.0 0.0
5 5.0 101.0 2.0 0.0 -2.0 99.0 0.0
6 6.0 99.0 4.0 0.0 -4.0 95.0 0.0
7 7.0 95.0 8.0 0.0 -8.0 87.0 0.0
8 8.0 87.0 16.0 0.0 -16.0 71.0 0.0
9 9.0 71.0 32.0 0.0 -32.0 39.0 0.0
Mieliśmy akurat pecha 😄, od 4 rzutu cały czas przegrywaliśmy i ostatecznie skończyliśmy z kwotą 39.0 ze 100 na początku. Gdybyśmy dalej stosowali tą strategie następnie musielibyśmy postawić kwotę 64.0, ale takiej kwoty już nie posiadamy.
Innym razem:
auto_run(game_count = "2.00",cash = 100, start_bet = 1, on_loss = 1, rolls = 10)
roll cash_before bet bancrupt result cash simulation
0 0.0 100.0 1.0 0.0 1.0 101.0 0.0
1 1.0 101.0 1.0 0.0 1.0 102.0 0.0
2 2.0 102.0 1.0 0.0 1.0 103.0 0.0
3 3.0 103.0 1.0 0.0 1.0 104.0 0.0
4 4.0 104.0 1.0 0.0 1.0 105.0 0.0
5 5.0 105.0 1.0 0.0 -1.0 104.0 0.0
6 6.0 104.0 2.0 0.0 2.0 106.0 0.0
7 7.0 106.0 1.0 0.0 1.0 107.0 0.0
8 8.0 107.0 1.0 0.0 -1.0 106.0 0.0
9 9.0 106.0 2.0 0.0 2.0 108.0 0.0
Tym razem wyśliszmy na plusie o 8.0 po 10 zakładach. Na takim pojedyńczym sprawdzeniu nie można oprzeć symulacji, ale można się poprzeć Prawem Wielkich Liczb.
„Z prawdopodobieństwem dowolnie bliskim 1 można się spodziewać, iż przy dostatecznie wielkiej liczbie prób danego zdarzenia lsowego będzie się dowolnie mało różniła od jego prawdopodobieństwa.”[1]
Zwiększając liczbę doświadczeń opartych na zdarzeniach losowych, możemy oczekiwać rozkładu wyników coraz lepiej odpowiadającego rozkładowi prawdopodobieństw zdarzeń (na przykład, przeprowadzając wielką liczbę rzutów symetryczną monetą, możemy oczekiwać że stosunek liczby „wyrzuconych” orłów do liczby wszystkich rzutów będzie bliski 0,5 (wartości prawdopodobieństwa); tym większe są na to szanse im większa jest liczba rzutów)
Zamiast opierać się na pojedyńczym zdarzeniu zwiększymy liczbę doświadczeń dzięki czemu będziemy mogli zobaczyć jak dana strategia ma się do rzeczywistości.
Automat
Automat wykonuje symulacje na zadaną liczbę uruchomień (runs) i zwraca uśrednione wartości dla każdego rzutu począwszy od 0 do rolls.
def auto_simulation(runs = 10,
start_bet = 1, cash = 100,
game_count = "2.00", rolls = 50,
on_loss = -1, on_win = -1):
"""
Simulate whole auto_run n-times (runs)
Returns: Cash plot and statistics for each roll.
"""
df = pd.concat([
auto_run(start_bet,cash,game_count,rolls,on_loss,on_win,simulation = i)
for i in range(runs)],ignore_index = True)
df = df.assign(profit = lambda x: x.cash - x.cash_before )
df = df.assign(profitr = lambda x: x.cash - cash)
import matplotlib.pyplot as plt
statistics = df.groupby(['roll']).agg(
{
'bet': { 'max': 'max',
'cnt': lambda x: (x[x==np.max(x)].count()) },
'bancrupt': {'%': lambda x: np.sum(x)/runs*100 },
'profit': { '': 'mean' },
'profitr': { '': 'mean' },
'cash': { '': 'mean',
'win.%': lambda x: (x[x>cash]).count()/runs*100,
'win': lambda x: (x[x>cash]-cash).mean(),
'loss.%': lambda x: (x[x<cash]).count()/runs*100,
'loss': lambda x: (x[x<cash]-cash).mean(),
},
}).round(decimals=2).reset_index()
statistics.columns = statistics.columns.map('.'.join).str.strip().str.rstrip('.')
statistics.insert(1, 'bet.maxr',statistics['bet.max'].cummax())
statistics.insert(2, 'bet.cntr', np.nan)
#calculate running sum for statistics
for s in statistics.index:
statistics.loc[s,'bet.cntr'] = statistics[
(statistics['bet.max'] == statistics.loc[s,'bet.maxr']) &
(statistics['roll']<=statistics.loc[s,'roll'])]['bet.cnt'].sum()
statistics['bet.cnt'] = statistics['bet.cnt']/runs*100
statistics['bet.cntr'] = statistics['bet.cntr']/runs*100
statistics = statistics.rename(index=str, columns = { 'bet.cnt': 'bet.%', 'bet.cntr': 'betr.%' })
plt.xlabel("rolls")
plt.ylabel("cash")
plt.plot(statistics[['cash']])
return statistics
Uruchomienie jej dla 10, 100, 1000 nie zwraca nam tendencji w wyniku, ale już przy 10,000 można pokusić się o tendencje i powtarzalność która jest niestety opadająca 😞 . Poniżej symulacja którą przeprowadziłęm dla 100000 uruchomień.
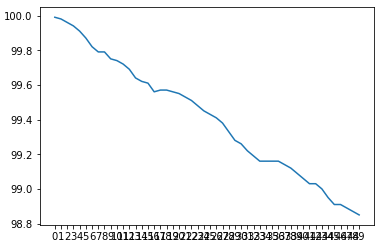
auto_simulation(runs=100000, game_count = "2.00",cash = 100, start_bet = 1, on_loss = 1, rolls = 10)
roll betr bet bancrupt profit profitr cash cash
maxr % max % % cash win% win loss% loss
0.0 1.0 100.000 1.0 100.000 0.00 -0.01 -0.01 99.99 49.57 1.00 50.43 -1.00
1.0 2.0 50.434 2.0 50.434 0.00 -0.01 -0.02 99.98 49.60 1.50 25.44 -3.00
2.0 4.0 25.445 4.0 25.445 0.00 -0.02 -0.04 99.96 62.03 1.79 25.37 -4.53
3.0 8.0 12.826 8.0 12.826 0.00 -0.02 -0.06 99.91 71.30 2.59 22.39 -8.64
4.0 16.0 6.530 16.0 6.530 0.00 -0.03 -0.09 99.91 71.30 2.59 22.39 -8.64
5.0 32.0 3.247 32.0 3.247 0.00 -0.04 -0.13 99.87 74.28 3.00 19.25 -12.26
...
41.0 64.0 0.001 32.0 1.278 27.22 -0.03 -0.97 99.03 70.79 20.10 29.14 -52.14
42.0 64.0 0.003 64.0 0.002 27.85 -0.00 -0.97 99.03 70.27 20.60 29.68 -52.02
43.0 64.0 0.003 32.0 1.211 28.44 -0.03 -1.00 99.00 69.66 21.11 30.31 -51.81
44.0 64.0 0.009 64.0 0.006 29.06 -0.05 -1.05 98.95 69.02 21.62 30.96 -51.60
45.0 64.0 0.018 64.0 0.009 29.71 -0.04 -1.09 98.91 68.42 22.14 31.57 -51.43
46.0 64.0 0.040 64.0 0.022 30.33 -0.01 -1.09 98.91 67.88 22.67 32.11 -51.32
47.0 64.0 0.066 64.0 0.026 30.93 -0.02 -1.11 98.89 67.31 23.19 32.68 -51.16
48.0 64.0 0.107 64.0 0.041 31.49 -0.02 -1.13 98.87 66.79 23.68 33.20 -51.03
49.0 64.0 0.165 64.0 0.058 32.01 -0.03 -1.15 98.85 66.21 24.20 33.77 -50.86
Kolumny:
- roll: Numer losowania od początku
- betr: Maksymalna stawka od początku (
maxr), i jak często się pojawiła (%) - bet Maksymalna stawka na dane losowanie (
max), i jak często się pojawiła w danym losowaniu(%) - bancrupt: Procent losowań w których stawka jest wyższa niższa posiadana kwota
- profit: Średni wynik losowania.
- profitr: Średnia nadwyżka od początkowej kwoty (
start_cash) - cash>: Kwota posiadana na dane losowanie
- win: Średnia nadwyższka od kwot które są powyżej początkowej puli i ich udział. (
%) - loss: Średnia strata od kwot które są poniżej początkowej puli i ich udział. (
%)
Wywnioskować można jedno, że zwykłe podwajanie kwoty nie pomaga i na każdą wygraną zdarzają się przegrane które umniejszają wynik. Dodatkowo średnio po 50 losowaniach 32% wszystkich uruchomień zostają z pieniędzmy mniejszymi niż wymagany zakład a więc z niemożliwością grania danej.
Jest to oczywiście bardzo prosty algorytm który w założeniach wydaje się że powinien przynosic zysk. Przecież za każdym razem podwajamy kwotę. Może mamy za małą kwotę początkową. I tutaj niestety też wszystkich zmartwie. Symulacja przy kwocie początkowej: cash = 100000 wygląda następująco:
max_bet: 32768.0 (0.062%)
profitr: -5.96
bancrupt: 0.03%
cash: 99994.04
cash win: 23.25 (96.62%)
cash loss: -850.61 (3.34%)
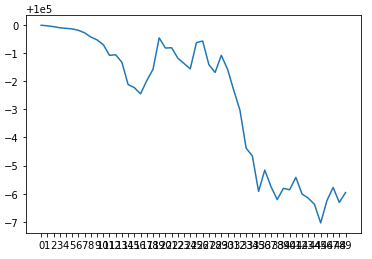
Tak więc przy kwocie przykładowo: 100,000$, i stawianiu na początku 1$ średnio tracimy 5.96$ po 50 rzutach. Wprawdzie liczba bankrutów się zmniejszyła, ale i tak istnieją zakłady które przekraczają podaną kwotę. Wynik to z prawdopodbieństwa. Jeśli przegranie 15 razy pod rząd przy prawdopobieństwie 0.5 (tutaj jest jeszcze większe bo wygrana w wariancie 2.0 wynosi 0.475) wynosi 2^15 = 32768 to na te 32768 przypadków taka systuacja powinna się pojawić co najmniej raz. Przegrana w takim wypadku przeważają nad możliwą wygraną i dlatego kasyna wygrywają. W przypadku innych wariantów czy zwiększaniu liczby kwot wykresy wyglądają niestety bardzo podobnie. Z tak prostej strategii prędzej czy póżniej przegramy.
Możemy wymyśleć inną strategię np: gramy podwająjąc kwotę dopóki nie uzbieramy określonej kwoty np: 10$.
Strategia dla zysku
W tym wypadku możemy zamiast ustawić stałą liczbę gry, ustawiamy profit=10 czyli zysk jaki chcemy uzyskać. Jedyne co zwracamy to w którym kroku przerwaliśmy grę, jaka była maksymalna stawka, i czy zbankrutowaliśmy. W przypadku wygrania powinniśmy mieć cash=cash + profit, ale w przypadku przegranej będzie to kwota która nam pozostała.
def cont_run(start_bet = 1, cash = 100, game_count = "2.00", profit = 10, on_loss = -1, on_win = -1, simulation = 0):
bet = start_bet
max_bet = start_bet
end_cash = cash + profit
roll = 0
while True:
roll += 1
cash_before = cash
if(cash_before < bet):
# roll, cash, max_bet, bancrupt
return [roll, cash, max_bet, 1.0]
result = play(bet, game_count)
cash += result
if(cash>=end_cash):
return [roll, cash, max_bet, 0.0]
bet = auto_method(start_bet,bet,result,on_loss,on_win)
if(bet>max_bet):
max_bet = bet
def cont_simulation(runs = 100,
start_bet = 1, cash = 100,
game_count = "2.00", profit = 10,
on_loss = -1, on_win = -1):
df = pd.DataFrame([
cont_run(start_bet,cash,game_count,profit,on_loss,on_win,simulation = i)
for i in range(runs)],
columns = ["rolls", "cash", "max_bet", "bancrupt"], dtype = float)
import matplotlib.pyplot as plt
statistics = df.groupby(["rolls"]).agg({
'max_bet': {
'mean': 'mean',
'max': 'max',
'%': lambda x: (x[x==np.max(x)].count())/runs * 100
},
'cash': { 'mean': 'mean', 'cnt': 'count' },
'bancrupt': {'': 'mean' }})
print('Mean profit:', statistics[('cash','mean')].mean() - cash)
print(f"% number of wins: {((1-statistics[('bancrupt','')].mean()) * 100):.2f}%")
plt.xlabel("rolls")
plt.ylabel("cash")
plt.plot(statistics[[('cash','mean')]],label="roll")
return statistics
Co pokazały symulacje. Że w przypadku 100$ i chęci zyskania 10$ średni zysk wacha się od -8$ do -10$
cont_simulation(runs = 10000000, game_count = "2.00",cash = 100, start_bet = 1, on_loss = 1, profit = 10)
Mean profit: -10.163005419483099
'%' number of wins: 70.23%
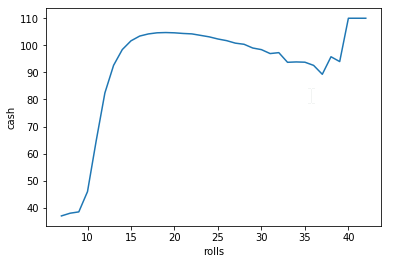
Co ciekawe im mniejsza ilość rzutów tym większa przegrana ale wynika to z początkowych licznych przegranych które zwiększyły stawka do wartości powyżej początkowej kwoty. Zwiększanie początkowej kwoty niewiele daje i powoduje że nawet mając milion dolarów to średnio i tak tracimy.
cont_simulation(runs = 10000000, game_count = "2.00",cash = 1000000, start_bet = 1, on_loss = 1, profit = 10)
Mean profit: -402.102759478963
'%' number of wins: 99.92%
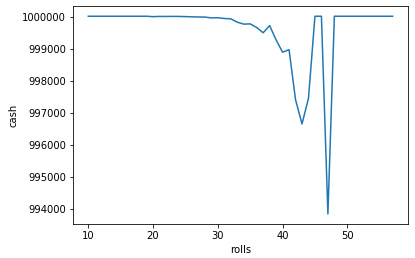
Wprawdzie procent szansy na wygraną jest większy, wynosi aż 99.92%, ale zdarzają się sytuacje w których przegrywasz i koniec końców kwota przegrana jest większa niż tyle ile wygrałeś do tej pory.
Strategia tablicowa
To była bardzo prosta strategia podwajania kwoty dopóki się nie wygra albo przegra z kretesem 😄. Może po każdym razie możemy zwiększać/zmniejszać kwotę w zależności od tego która to jest przegrana z kolei co pozwoli w pewnym sensie zminimalizować przegraną. Nazwałem to strategią tablicową. I jedyną zmianą w stosunki do strategii dla zysku jest lista on_loss/on_win która posiada dwie wartości, o ile zwiększyć/zmniejszyć wartość zakładu i jaką grę ustawić.
W tym wypadku wystarczy skopiować poprzednie funkcje i nieco je zmodyfikować tak żeby brały przykład z on_loss i on_run jako tablicę. Jeżeli nie wskażemy powrotu do wartości początkowej przez -1 będzie on grał według ostatniego elementu.
def table_run(start_bet = 1, cash = 100, game_count = "2.00",
profit = 10,
on_loss = [[-1, "2.00"]],
on_win = [[-1, "1.50"]], simulation = 0):
bet = start_bet
max_bet = start_bet
end_cash = cash + profit
loss_cnt = 0
win_cnt = 0
game_current = game_count
element = []
roll = 0
while True:
roll += 1
cash_before = cash
if(cash_before < bet):
# roll, cash, max_bet, bancrupt
return [roll, cash, max_bet, 1.0]
result = play(bet, game_current)
cash += result
if(cash>=end_cash):
return [roll, cash, max_bet, 0.0]
if result <= 0:
element = on_loss[-1] if len(on_loss) <= loss_cnt else on_loss[loss_cnt]
win_cnt = 0
loss_cnt += 1
else:
element = on_win[-1] if len(on_win) <= win_cnt else on_win[win_cnt]
loss_cnt = 0
win_cnt += 1
bet = start_bet if element[0] < 0 else bet + bet * element[0]
game_current = element[1]
if element[0]<0: #return to start
loss_cnt = 0
win_cnt = 0
#print(f"{roll:5.0f}: {cash_before:>8}$ |game: {game_current} bet: {bet:4.2f}| loss:{loss_cnt:2.0f} win: {win_cnt:2.0f} result: {result:>4} {cash:>8}$ e: {element}")
if(bet>max_bet):
max_bet = bet
def table_simulation(runs = 100,
start_bet = 1, cash = 100,
game_count = "2.00", profit = 10,
on_loss = [[-1, "2.00"]],
on_win = [[-1, "2.00"]]):
df = pd.DataFrame([
table_run(start_bet,cash,game_count,profit,on_loss,on_win,simulation = i)
for i in range(runs)],
columns = ["rolls", "cash", "max_bet", "bancrupt"], dtype = float)
import matplotlib.pyplot as plt
statistics = df.groupby(["rolls"]).agg({
'max_bet': {
'mean': 'mean',
'max': 'max',
'%': lambda x: (x[x==np.max(x)].count())/runs * 100
},
'cash': { 'mean': 'mean', 'cnt': 'count' },
'bancrupt': {'': 'mean' }})
print('Mean profit:', statistics[('cash','mean')].mean() - cash)
print(f"% number of wins: {((1-statistics[('bancrupt','')].mean()) * 100):.2f}%")
plt.xlabel("rolls")
plt.ylabel("cash")
plt.plot(statistics[[('cash','mean')]],label="roll")
return statistics
Wywołanie funkcji z takimi parametrami to taka naprawde poprzednia omawiana prosta strategia podwajania wartości za każdym razem gdy przegramy.
table_run(start_bet = 1, cash = 100, game_count = "2.00",
profit = 10,
on_loss = [[1, "2.00"]],
on_win = [[-1, "2.00"]], simulation = 0)
100$ |game: 2.00 bet: 1.00| loss: 0 win: 0 result: 1.0 101.0$ e: [-1, '2.00']
101.0$ |game: 2.00 bet: 1.00| loss: 0 win: 0 result: 1.0 102.0$ e: [-1, '2.00']
102.0$ |game: 2.00 bet: 1.00| loss: 0 win: 0 result: 1.0 103.0$ e: [-1, '2.00']
103.0$ |game: 2.00 bet: 2.00| loss: 1 win: 0 result: -1 102.0$ e: [1, '2.00']
102.0$ |game: 2.00 bet: 1.00| loss: 0 win: 0 result: 2.0 104.0$ e: [-1, '2.00']
104.0$ |game: 2.00 bet: 2.00| loss: 1 win: 0 result: -1 103.0$ e: [1, '2.00']
103.0$ |game: 2.00 bet: 1.00| loss: 0 win: 0 result: 2.0 105.0$ e: [-1, '2.00']
105.0$ |game: 2.00 bet: 1.00| loss: 0 win: 0 result: 1.0 106.0$ e: [-1, '2.00']
106.0$ |game: 2.00 bet: 1.00| loss: 0 win: 0 result: 1.0 107.0$ e: [-1, '2.00']
107.0$ |game: 2.00 bet: 1.00| loss: 0 win: 0 result: 1.0 108.0$ e: [-1, '2.00']
108.0$ |game: 2.00 bet: 2.00| loss: 1 win: 0 result: -1 107.0$ e: [1, '2.00']
107.0$ |game: 2.00 bet: 4.00| loss: 2 win: 0 result: -2 105.0$ e: [1, '2.00']
105.0$ |game: 2.00 bet: 1.00| loss: 0 win: 0 result: 4.0 109.0$ e: [-1, '2.00']
109.0$ |game: 2.00 bet: 2.00| loss: 1 win: 0 result: -1 108.0$ e: [1, '2.00']
108.0$ |game: 2.00 bet: 4.00| loss: 2 win: 0 result: -2 106.0$ e: [1, '2.00']
106.0$ |game: 2.00 bet: 8.00| loss: 3 win: 0 result: -4 102.0$ e: [1, '2.00']
Out: [17, 110.0, 8, 0.0]
Sprawdżmy teraz kilka strategii, powiedzmy że zwiekszamy swoje prawdopodobieństwo za każdym razem gdy przegramy.
table_simulation(runs=10000,
start_bet = 1, cash = 10000, game_count = "2.00",
profit = 10,
on_loss = [[0.03, "1.98"], [3.1,"1.50"], [3.7, "1.32"], [12.17, "1.10"], [10, "1.10"], [-1,"2.00"] ],
on_win = [[-1, "2.00"]])
Warto wspomnieć że pod koniec wymagana jest kwota 2875.39 po 5 przegranie.
| przegrana | gra | szansa wygranek | mnożnik | stawka | do wygrania | łączna stawka | różnica |
|---|---|---|---|---|---|---|---|
| 0 | 2.00 | 49.50% | 1.00 | 2.00 | -1.00 | 1.00 | |
| 1 | 1.98 | 50.00% | 0.03 | 1.03 | 2.04 | -2.03 | 0.01 |
| 2 | 1.50 | 66.00% | 3.10 | 4.22 | 6.33 | -6.25 | 0.08 |
| 4 | 1.32 | 75.00% | 3.70 | 19.85 | 26.20 | -26.10 | 0.10 |
| 5 | 1.10 | 90.00% | 12.17 | 261.40 | 287.54 | -287.50 | 0.04 |
| 6 | 1.10 | 90.00% | 10.00 | 2875.39 | 3162.93 | -3162.89 | 0.04 |
Aby nie przegrać kwoty rosną bardzo szybko za każdym razem kiedy przegramy. Gdybyśmy od początku grali mając szanse 1/10 i zwiększając 10krotnie to przy szóstym podejściu potrzebowalibyśmy kwoty rzędu 10^6, a to oznacza pewną przegraną.
Symulacja jednak pokazuje że niewiele to pomogło, a spowodowało tylko przedłużenie ilości rzutów do kilkudziesięciu tysięcy.
Mean profit: -3815.467734336913
'%' number of wins: 53.09%
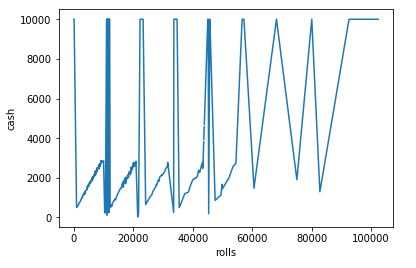
Oczywiście można sobie testować różne strategie, bo nie jestem w stanie wymyśleć i zasymulować wszystkich możliwości 😄 , ale może ktoś odkryje jakąś kombinacje przy której zysk jest większy od 0. Nie warto testować go na mniejszą ilość niż 100,000. Dopiero od tych ilości wyniki zdają się dążyć do jednej wartości.
Labouchere
Na koniec system który jest bardzo popularnym systemem w zakładach typu ruletka. Oprócz niego istnieje jeszcze pewnie kilkadziesiąt innych na których opis nie starczyłoby miesca. System ten wywodzi się od francuskiego filozofa i polega ona na zapisie naszej docelowej kwoty którą chcemy wygrać w postaci sumy liczb. Powiedżmy że chcemy wygrać 15$ , więc podzieliliśmy naszą wygrane na 5 liczb 1,2,3,4,5, ustawienie liczb i kolejność dostosowujemy sobie sami.
- Na początku stawiamy sumę skrajnych do siebe cyfr (w tym przypadku
1+5=6). - W przypadku wygranej kasujemy obydwie liczby z listy. (zostaje nam
2,3,4) - W przypadku przegranej dodajemy do listy kwotę którą postawiliśmy na sam koniec listy (
1,2,3,4,5,6) - Powtarzamy punkty od
1do3aż nie wyczyścimy całej listy.
Wydaje się proste, ale ma oczywiście haczyk jeśli będziemy ciągle przegrywać kwoty dopisywane do listy mogą się niebezpiecznie powiększyć.
W Python cały algorytm przedstawia się następująco:
W tym wypadku wystarczą tylko dwa parametry:
- cash - kwota początkowa
- system - wybrany system
A to co nam zwraca to tak jak poprzednio:
- roll - za którym razem udało się wygrać lub przegrać poniżej wartości wymaganej
- cash - końcowa kwota, jeśli wygrywamy powinna wynieść więcej o sumę poprzedniego zakładu
- max_bet - maksymalny postawiona stawka
- system - lista końcowa.
def labouchere_run(cash = 100, system = [1,2,3,4,5]):
game_count = "2.00"
roll = 0
max_bet = 0
system = system.copy()
#print(f"{roll:5.0f}: list: {system}")
while True:
roll += 1
cash_before = cash
# only if there is only two elements in the list
bet = system[0] + (system[-1] if len(system)>1 else 0)
if bet > max_bet:
max_bet = bet
if bet>cash:
return [roll, cash, max_bet, 1.0, system]
result = play(bet, game_count)
cash += result
if result>0:
if(len(system)>1):
system.pop(-1)
system.pop(0)
else:
system.append(bet)
if len(system)<=0:
return [roll, cash, max_bet, 0.0,[]]
#print(f"{roll:5.0f}: {cash_before:>8}$ |bet: {bet:4.2f}| result: {result:>4} {cash:>8}$ list: {system}")
No i w tym wypadku uruchomimy dla prostej sytuacji.
labouchere_run(100,system = [1,2,3,4,5])
1: 100$ |bet: 6.00| result: -6 94$ list: [1, 2, 3, 4, 5, 6]
2: 94$ |bet: 7.00| result: 7.0 101.0$ list: [2, 3, 4, 5]
3: 101.0$ |bet: 7.00| result: -7 94.0$ list: [2, 3, 4, 5, 7]
4: 94.0$ |bet: 9.00| result: 9.0 103.0$ list: [3, 4, 5]
5: 103.0$ |bet: 8.00| result: -8 95.0$ list: [3, 4, 5, 8]
6: 95.0$ |bet: 11.00| result: -11 84.0$ list: [3, 4, 5, 8, 11]
7: 84.0$ |bet: 14.00| result: 14.0 98.0$ list: [4, 5, 8]
8: 98.0$ |bet: 12.00| result: -12 86.0$ list: [4, 5, 8, 12]
9: 86.0$ |bet: 16.00| result: 16.0 102.0$ list: [5, 8]
Out[1210]: [10, 115.0, 16, 0.0, []]
Wow :happy:, wygraliśmy. Największy zakład jaki był to 16.0, a wystarczyło do tego 10 rzutów. Czas przyjrzeć się dla większej ilości w postaci symulacji.
Symulacja:
def labouchere_simulation(runs = 100,
cash = 100, system = [1,2,3,4,5]):
labouchere_result = [labouchere_run(cash,system) for i in range(runs)]
df = pd.DataFrame(labouchere_result,
columns = ["rolls", "cash", "max_bet", "bancrupt", "list"], dtype = float)
import matplotlib.pyplot as plt
statistics = df.groupby(["rolls"]).agg({
'max_bet': {
'mean': 'mean',
'max': 'max',
'%': lambda x: (x[x==np.max(x)].count())/runs * 100
},
'cash': { 'mean': 'mean', 'cnt': 'count' },
'bancrupt': {'': 'mean' }})
print('Mean profit:', statistics[('cash','mean')].mean() - cash)
print(f"% number of wins: {((1-statistics[('bancrupt','')].mean()) * 100):.2f}%")
max_bet_index = df['max_bet'].idxmax()
print('Max bet:', df.loc[max_bet_index,'max_bet'], ' with cash: ' , df.loc[max_bet_index,'cash'], ' from list: ', df.loc[max_bet_index,'list'] )
plt.xlabel("rolls")
plt.ylabel("cash")
plt.plot(statistics[[('cash','mean')]],label="roll")
return statistics
Z kwotą rzędu 100 uruchomienie kilka razy dla 100,000 uruchomień daje podobny wynik wynoszący:
Mean profit: -29.09197655642062
'%' number of wins: 52.72%
Max bet: 64.0 with cash: 3.0 from list: [16, 16, 32, 48]
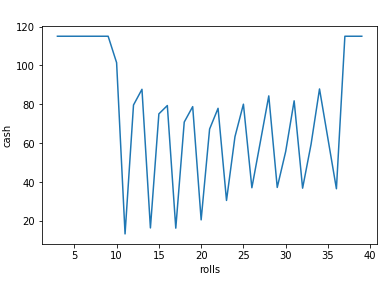
Średnio z taką kwotą nie przechodzimy powyżej 40 rzutów, ponieważ wtedy sumy do postawienia przekraczają kwotę 100 którą mamy na początku. Warto sprawdzić czy dla większej kwoty, np: 100,000 mamy podobne wyniki.
Wyższa kwota pozwoliła nam zwiększyć szanse na wygraną do 70.30%, ale w ostatecznym rozrachunku spowodowała też dużą ilość przegranych które na końcu pomniejszają twój zysk.
Mean profit: -25861.195673955735
'%' number of wins: 70.30%
Max bet: 55552.0 with cash: 2799.0 from list: [13888, 13888, 27776, 41664]
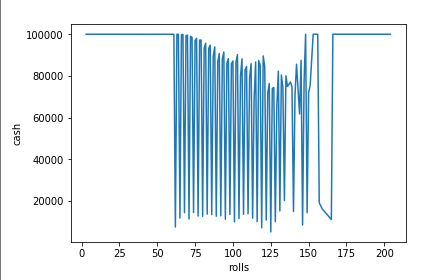
Systemami można się pobawić, ale nie znalazłem takiego który dla większej ilości symulacji powodowałby wyrównanie średniego zysku.
Wnioski
Po tych wszystkich strategiach i symulacjach niestety nie udało mi się znaleść idealnego rozwiązania. Wprawdzie duża ilość gotówki (w stosunku 1 milion do 1) gwarantuje większe szanse na wygrane (nawet 99%), ale jeśli żle się trafi co w przypadku większej ilości symulacj się zdarza powoduje przegranie całej kwoty.
Może się wydawać że niemożliwością jest przy 50% szansie na wygraną przegrać 6 do 12 razy pod rząd. Należy pamiętać że losowanie nie pamięta poprzednich wartości i zgodnie z prawem wielkich liczb dopiero przy dużej liczbie losowań całość zbiega do jakieś statystycznej średniej. Dodatkowo można pomyśleć żę skoro raz już przegraliśmy 6 razy pod rząd to drugi raz taka szansa się nie zdarza i tutaj także okazuje się system inaczej wyruwnóje szanse. Jak widać z pierwszych symulacji na automacie 8 razy pod rząd przegrana zdarza się, a wykładnicze powielanie kwoty tak aby wygrać albo by nie móc przegrać powoduje zwiększenie wymaganych pieniędzy do sporych wartości.
Inne systemy jak Labouchere czy tablicowy który miał pomniejszyć trochę stawki za każdym razem gdy przegramy nie spowodowały niestety poprawy. Niektóre systemy w dużej perspektywie dają 70% na wygraną co wydaje się żę jeśli więcej niż połowa to dobrze 😃, ale nie przewidują że może to oznaczać także duże przegraną jeśli akurat nie mieliśmy szczęścia.
W odpowiedzi na odwiecznie pytanie: Czy da się wygrywać na loterii?

Załączniki
Źródła
Labouchere: http://www.surebety.pl/artykul/labouchere
Ada Loverence:
https://en.wikipedia.org/wiki/Ada_Lovelace
https://www.famousscientists.org/ada-lovelace/
https://gadzetomania.pl/58233,ada-lovelace-pierwsza-programistka
Video
Labouchere, by “Sentdex”: https://www.youtube.com/watch?v=bUFQNjjItok
Gambling paradox, by “Looking Glass Universe: https://www.youtube.com/watch?v=t8L9GCophac
Why the Martingale Betting System Doesn’t work, by “Looking Glass Universe”https://www.youtube.com/watch?v=Ry3B9hJbBfk&t=4s
Książki
“Orzeł czy Reszka”- Hugo Steinhaus, ISBN 978-83-01-16284-9